Katalog znanja je določil Strokovni svet Republike Slovenije za splošno izobraževanje na 89. seji dne 31. 3. 2006.
Matematika kot veda, ki je neločljivo povezana z drugimi vedami in vsemi področji življenja, ima pomembno vlogo v splošnem izobraževanju posameznika. Pouk matematike je pomemben, ker pri njem dijaki spoznavajo in razvijajo zahtevnejše načine razmišljanja (npr. deduktivno razmišljanje) ter hkrati spoznavajo matematične pojme in postopke, ki so nepogrešljivi za vključenost in delovanje v sodobni družbi.
Pouk matematike v srednjem strokovnem izobraževanju upošteva značilnosti posameznih strokovnih področij in potrebe dijakov.
Vsa strokovna področja so vse bolj matematizirana, vendar pa je matematika v njih čedalje manj vidna, saj se skriva v tehnologiji (računalniških programih, matematičnih modelih, strojih in izdelkih). Za opravljanje določenih dejavnosti je zato vedno manj pomembno obvladovanje računanja in določenih matematičnih postopkov, vedno pomembnejša pa sta razumevanje matematičnih pojmov, sposobnost povezovanja matematičnega znanja z danimi situacijami na nekem strokovnem področju in zmožnost reševanja strokovnih problemov. To je osnova za kompetentno uporabo tehnoloških orodij, ki so danes na voljo in ki opravijo večji del osnovnih matematičnih postopkov.
Za dijake, ki zaključijo srednje strokovno izobraževanje, je pomembno dvoje. Na eni strani naj jim pridobljeno matematično znanje in kompetence, ki jih razvijejo, nudijo stabilno orientacijo v opravljanju dejavnosti na lastnem strokovnem področju, na drugi strani pa naj bo to znanje dovolj splošno, da jim omogoča nadaljnje izobraževanje. Pri pouku matematike je treba upoštevati tudi strukturo dijakov, njihove specifičnosti in možnosti, ter dejavnosti pri pouku organizirati na tak način, da so dijakom dovolj blizu, povezane s specifiko njihove stroke, z drugimi področji in z življenjem. Dijake vzgajamo tudi k natančnosti, sistematičnosti, doslednosti, urejenosti in vztrajnosti pri delu.
Ključne kompetence se udejanjajo skozi ključne kompetence predmeta matematika, ki izhajajo iz globalnih ciljev predmeta in so zapisane v III. poglavju v razdelku 3.2.
Cilje matematike v srednjih strokovnih šolah dosegamo z razvijanjem določenih ključnih kompetenc; zapisane so v nadaljevanju skupaj z osnovnimi smernicami za doseganje.
V srednjih strokovnih šolah pri poučevanju uporabljamo različne pristope, pri čemer glede na obravnavano temo izberemo najustreznejšega:
Pouk matematike naj upošteva povezave s stroko in drugimi področji. Te povezave so večstranske in večplastne:
Pri vseh načinih uvajanja pojmov, še posebej pa v zadnjem primeru, je nujno sodelovanje med učiteljem matematike drugimi učitelji, ki naj temelji na načelih timskega dela.
Tako za uspešno poklicno delo na izbranem strokovnem področju kot tudi za uspešno nadaljnje izobraževanje je pomembna zmožnost kompetentne uporabe tehnologije pri reševanju matematičnih problemov. Zato se dijaki pri pouku matematike učijo uporabe navadnih in grafičnih računal ter računalniških programov in jih uporabljajo. Uporablja se različna računalniška orodja, npr.: programe dinamične geometrije, programe za simbolno računanje, računalniške preglednice, programe za tridimenzionalno modeliranje, programe za obravnavo specifičnih učnih vsebin in druge, na posameznem strokovnem področju uveljavljene programe, ki omogočajo učenje ali uporabo matematike.
Uporaba tehnologije omogoča obravnavo kompleksnejših in realističnih situacij ter učenje zahtevnejših matematičnih strategij. Zmožnost uporabe tehnologije je pomembna tudi za uspešno delo pri drugih predmetih. Tehnologijo pri pouku matematike uporabljamo tudi zato, da omogočimo učenje matematike dijakom, ki bi jih skromnejše računske spretnosti ali specifični primanjkljaji v znanju ovirali pri nadaljnjem učenju.
Učitelj matematike na srednji strokovni šoli naj bo del »strokovnega okolja« na šoli. Biti mora dobro seznanjen s strokovnim področjem, za katerega se dijaki izobražujejo. Poznati mora tehnologijo njihove dejavnosti, terminologijo, dogovore in oblike dela, organizacijo dela idr., ker bo le tako znal avtentično in verodostojno vključevati elemente strokovnega področja v pouk matematike. Na ta način bo bolje razumel dijake in tudi dijaki bodo laže sprejemali njega in matematiko, ki jo poučuje, kot pomemben sestavni del svoje stroke in življenja.
Učitelj matematike naj timsko sodeluje z učitelji stroke in drugih predmetov pri načrtovanju in izvajanju pouka. Kot član tima poglablja svoj uvid v stroko in druge predmete, sam pa drugim učiteljem približa filozofijo pouka matematike in matematične kompetence, pomembne za uspešno delovanje in napredovanje dijakov pri izobraževanju, na strokovnem področju in v vsakdanjem življenju. Načrtovanje dejavnosti in pouka je tako usklajeno in smiselno ter dijakom omogoča ustrezen razvoj matematičnega znanja in kompetenc.
Za uspešen razvoj kompetenc je pomembno, da med udeleženci učnega procesa vlada spoštljiv in korekten odnos, v katerem so jasno razmejene pravice in odgovornosti tako učitelja kot dijakov. Dijaki naj imajo možnost sodelovati pri načrtovanju aktivnosti za pouk matematike in naj sodelujejo tudi pri pripravi teh aktivnosti (priprava materialov ali iskanje gradiv). Učitelji matematike naj dijake usmerjajo v reflektirane aktivnosti in kritično razmišljanje ter jim dajejo možnost izbiranja in odločanja. S takšnim pristopom dijaki razvijajo višjo mero odgovornosti za lastne odločitve in lastno znanje.
Posamezne teme vsebujejo več tematskih sklopov. Nekateri tematski sklopi so obvezni za vse programe SSI, nekateri pa so izbirni.
Izbirni tematski sklopi so posebej označeni in se obravnavajo po izbiri programa ali šole glede na posebnosti in potrebe različnih strok. Za uresničevanje izbirnih tematskih sklopov je treba zagotoviti dodatne ure pouka matematike.
Ker struktura matematičnega znanja temelji na notranjih povezavah, je za poučevanje in učenje matematike v srednji strokovni šoli izjemnega pomena, da se novo znanje gradi na predhodnem. Še posebej je pomembno navezovanje matematičnega znanja na predznanje dijakov ob prehodu iz osnovne v srednjo šolo. Zato so na začetku tistih tematskih sklopov, ki so neposredna nadgradnja osnovnošolskega programa matematike, navedeni matematični pojmi, vsebine in simboli, ki sodijo v temeljno matematično znanje učencev ob zaključku osnovne šole. Navedene pojme in vsebine so dijaki v osnovni šoli obravnavali, seveda pa je razumno pričakovati, da so jih nekateri učenci usvojili pomanjkljivo ali so jih pozabili. Učitelj ne poučuje ponovno tistih vsebin, ki sodijo v pričakovano predznanje dijakov, ampak pripravi ustrezne dejavnosti za samostojno delo dijakov doma in/ali v šoli, pri katerih dijaki predznanje obnovijo in dopolnijo. Učitelj diagnosticira napačne predstave in primanjkljaje ter dijakom pomaga, da jih odpravijo.
Učitelj na začetku šolskega leta pripravi ustrezne dejavnosti za samostojno delo dijakov, ki dijakom omogočajo pregledno ponovitev in sistemiziranje matematičnega znanja. Na začetku nove teme ali tematskega sklopa pa so dejavnosti za samostojno delo dijakov namenjene ponovitvi tistih matematičnih osnov, ki so pomembne za učenje novih vsebin. Učitelj pomaga dijakom odpraviti napačne predstave ali primanjkljaje v znanju.
| 1.1 Osnovna znanja o številih |
Povezani cilji iz OŠ:
Dijak pozna naravna,cela, racionalna in realna števila, loči te množice števil in razume odnos med njimi (N⊂Z⊂Q⊂R).
Števila predstavi na različne načine (s števkami, z besedami, s točkami na številski premici). Na številski premici uredi števila. Pozna imena računskih
operacij in uporablja osnovne računske zakone pri računanju vrednosti številskih izrazov. Računa z navadnim računalom. Danemu številu določi
nasprotno in obratno število. Ulomek izrazi v decimalni obliki, razlikuje končna in periodična decimalna števila in pretvarja decimalna števila v desetiški
ulomek.
Pozna pojem delitelja in večkratnika. Določa delitelje, večkratnike, največji skupni delitelj in najmanjši skupni večkratnik za »majhna« števila. Loči soda
in liha števila in pozna kriterije deljivosti s števili: 2, 5, 3, 9, 10 in 10n. Pozna potenco z naravnim eksponentom in računa s takimi potencami.
Rešuje preproste neenačbe.
Računa z izrazi s spremenljivkami: sešteva, odšteva, množi veččlenike, računa kvadrat dvočlenika, produkt vsote in razlike dveh členov. Izpostavlja
skupni faktor in razstavi razliko kvadratov. Računa vrednost izraza s spremenljivkami za dane vrednosti spremenljivk.
Dijak pozna pojem odstotek. Pozna pojem premo in obratno sorazmerne količine. Uporablja sklepni račun.
Dijak pozna pojem kvadratni koren in določa kvadratne korene (popolnih kvadratov) na pamet in s pomočjo navadnega računala.
Dijak pozna pojem absolutne vrednosti števila in določa absolutno vrednost števila. |
Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi osnovne pojme,
postopke in operacije s števili
(iz OŠ).
|
|
Učitelj izdela načrt dejavnosti, s katerimi dijaki
samostojno ponovijo osnovne pojme, postopke in
operacije s števili. Učitelj diagnosticira in po potrebi
dopolni vrzeli ali napačne predstave v znanju dijakov. |
| Dijak pozna naravna, cela,
racionalna in realna števila in
uporablja različne
predstavitvene oblike števil. |
Dijak pretvarja periodična decimalna števila v okrajšani
ulomek. |
Pojme in različne načine predstavitve števil dijaki
uporabljajo pri reševanju problemov, v pogovorih o
matematiki, diskusijah, razlagah.
Upoštevajmo, da nimajo predznanja pri pretvarjanju
periodičnih decimalnih števil v ulomke. |
| Dijak pozna pojem potenca in
računa s potencami z naravnimi
in celimi eksponenti. |
Dijak pozna pravila za računanje s potencami in jih
uporablja pri računanju vrednosti številskih izrazov.
Uporablja pravila za računanje s potencami v
algebrskih izrazih.
Razume potenco 10-n in uporablja zapis decimalnega
števila v potenčni obliki
(npr: 0,1 =10-1 , 0,02 = 2×10-2 ).
Dijak zaokroži decimalno število poljubno natančno
(npr.: na celo število, dve decimalki, tisočino, dve
mesti). |
Dijaki poiščejo primere zapisov potenc pri drugih
predmetih, v stroki in okolju. Ugotavljajo pomen,
smiselnost, korektnost in uporabnost zapisov potenc.
Za računanje vrednosti številskih izrazov uporabljajo
navadno računalo. |
Dijak računa v množicah
N,Z,Q,R |
Dijak razume in uporablja imena računskih operacij,
uporablja osnovne računske zakone pri računanju
vrednosti številskih izrazov, upošteva vrstni red operacij
in pravilno ter zanesljivo uporablja navadno računalo.
Razlikuje tri pomene znaka minus.
Oceni rezultat in kritično vrednoti dobljeno rešitev. |
Poudarek naj bo na urjenju znanih računskih operacij,
ocenjevanju pričakovanega rezultata in kritičnem
vrednotenju dobljene rešitve. Osnovne računske
operacije dijak izvaja pisno, ustno in z uporabo
navadnega računala.
Dijak rešuje probleme, ki izhajajo iz življenjskih in
poklicnih situacij. |
Dijak uredi števila in računa z
neenakostmi. |
Dijak uredi števila po velikosti in jih predstavi na
številski premici (realni osi). Dijak razume pomen
znakov za neenakosti: večji, večji ali enak, manjši,
manjši ali enak (>, ≥, <, ≤) in jih uporablja. Uporablja
lastnosti relacije urejenosti in pravila za računaje z
neenakostmi. Rešuje preproste neenačbe. |
Poudarek naj bo na predstavitvi urejenosti števil na
realni osi.
Dijaki naj uporabljajo znake za neenakosti. |
Dijak računa z algebrskimi
izrazi. |
Dijak izračuna vrednost izraza s spremenljivkami.
Poenostavi izraz s spremenljivkami (sešteva, odšteva in
množi enočlenike in veččlenike).
Računa kvadrat in kub dvočlenika in razstavlja
preproste algebrske izraze. Pri tem uporablja
operacije: izpostavljanje skupnega faktorja,
razstavljanje razlike kvadratov, razlike in vsote kubov
ter razstavljanje tričlenikov po Vietovem pravilu.
Izvaja operacije s preprostimi algebrskimi ulomki.
Poenostavlja sestavljene (dvojne) ulomke in računa z
njimi. |
Upoštevati moramo, da dijaki iz OŠ poznajo le
kvadriranje dvočlenika in produkt vsote in razlike dveh
členov.
Najprej dobro utrdimo posamezne izraze.
Dijak naj računa tudi s »sestavljenimi« izrazi
(kvadriranje, kubiranje, množenje, razstavljanje …).
Urjenje lahko učinkovito poteka v skupinah.
Spozna naj tudi računalniške programe za simbolno
računanje.
Poudarek je na krajšanju in razširjanju algebrskih
ulomkov. |
| Dijak določi delitelje in
večkratnike števila. |
Dijak uporablja pojma delitelj in večkratnik, določi
delitelje in večkratnike števila ter število razstavi v
produkt praštevil. Razlikuje praštevila in sestavljena
števila.
Uporablja kriterije deljivosti s števili: 2, 3, 4, 5, 6, 8, 9
in 10n. |
Dijaki naj pred obravnavo v šoli samostojno ponovijo
znane pojme iz osnovne šole (domače delo).
Poudarimo razločevanje med izrazoma n×a (večkratnik) in an (potenca). |
| Dijak pozna osnovni izrek o
deljenju. |
Dijak pozna relacijo deljivosti in razume osnovni izrek o
deljenju. Uporablja osnovni izrek o deljenju za
reševanje nalog iz vsakdanjega življenja. |
Dijaki naj rešujejo tekstne naloge iz vsakdanjega
življenja, pri katerih uporabijo osnovni izrek o deljenju. |
| Dijak določi skupne delitelje in
večkratnike števil. |
Dijak določi skupne delitelje ter največji skupni delitelj
dveh ali več števil s poskušanjem in z razcepom.
Določi skupne večkratnike in najmanjši skupni
večkratnik dveh ali več števil s poskušanjem in z
razcepom.
Pozna relacijo deljivosti in razume pojem tuji si števili. |
Dijaki samostojno ponovijo znane pojme iz OŠ. Po
presoji učitelja dijak spozna in uporablja tudi Evklidov
algoritem za računanje največjega skupnega delitelja.
Najmanjši skupni večkratnik izračuna s formulo
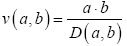 . . |
| Dijak uporablja procentni
račun. |
Dijak pozna in razume pojem odstotek in promila in ju
poveže z odnosom med deležem in celoto.
Računa procentno mero, delež ali osnovo in uporablja
procentni račun v vsakdanjih situacijah in v stroki. |
Preverimo poznavanje iz OŠ.
Dijaki naj poiščejo primere uporabe pojmov v
vsakdanjem življenju in stroki.
Tematika naj bo obravnavana tudi v okviru
medpredmetnih projektov. Uporaba navadnega
računala naj služi učinkovitemu računanju. |
| Dijak uporablja pojem
razmerje. Dijak razlikuje premo
in obratno sorazmerne količine. |
Dijak pozna, razume in uporablja pojem razmerje v
različnih kontekstih in situacijah. Analizira odnos med
količinama in ugotovi, ali sta količini premo ali obratno
sorazmerni, ter rešuje probleme na poljuben način
(npr. s sklepanjem). |
Učitelj preveri predznanje in da poudarek reševanju
nalog iz stroke. Dijak rešuje probleme, ki izhajajo iz
življenjskih in poklicnih situacij. |
| Dijak razume razširitev množice
racionalnih števil z
iracionalnimi števili. |
Dijak razume obstoj števil, ki se ne dajo zapisati z
ulomkom. Ponazori iracionalno število na realni osi. |
Po presoji učitelja naj se izvede dokaz, da obstajajo
števila, ki se ne dajo zapisati z ulomkom. |
| Dijak razume odnos med
kvadratnim korenom in
kvadratom števila. |
Dijak razume odnos med kvadratnim korenom in
kvadratom števila. Računa kvadratne korene popolnih
kvadratov (do 20) na pamet, oceni kvadratni koren
poljubnega števila in računa korene z navadnim
računalom. |
Preverimo predznanje. |
| Dijak razume odnos med
kubičnim korenom in kubom
števila. |
Dijak razume odnos med kubičnim korenom in kubom
števila ter računa korene z navadnim računalom. |
Upoštevamo, da dijaki nimajo predznanja. |
| Dijak računa s koreni. |
Dijak računa vrednosti izrazov, v katerih nastopajo
kvadratni in kubični koreni, smiselno ocenjuje
pričakovani rezultat in kritično vrednoti dobljeno
rešitev. Pravilno in zanesljivo uporablja navadno
računalo in računa z določeno natančnostjo. Uporablja
delno korenjenje in racionalizacijo imenovalca pri
računanju točnih vrednosti izrazov. Poenostavlja
algebrske izraze s koreni. |
Poudarimo kritično ocenjevanje vmesnih in končnih
rezultatov. |
| Dijak pozna pojem interval. |
Dijak pozna pojem interval in predstavi oz. zapiše
interval na različne načine: grafično na realni osi, z
uporabo znakov za neenakosti, z množicami.
Dijak rešitev neenačbe zapiše z intervalom. |
Dijaki uporabljajo različne simbolne zapise intervalov. |
| Dijak pozna in razume pojem
absolutna vrednost realnega
števila |
Dijak pozna in razume definicijo absolutne vrednosti.
Upošteva lastnosti absolutne vrednosti in računa z
izrazi, v katerih nastopajo absolutne vrednosti. Rešuje
preproste enačbe in neenačbe z absolutno vrednostjo.
Loči med absolutno in relativno napako. |
Poudarimo »geometrijsko« ponazoritev absolutne
vrednosti. Rešujemo le številske izraze z absolutno
vrednostjo in preproste enačbe ter neenačbe.
Poudarimo uporabo določanja absolutne in relativne
napake v stroki. |
| Dijak pozna korene poljubnih
stopenj in računa z njimi. |
Dijak računa korene višjih stopenj na pamet in z
navadnim računalom. Poenostavlja številske in
algebrske izraze, v katerih nastopajo koreni višjih
stopenj. |
Dijak naj se nauči uporabljati navadno računalo pri
računanju s koreni višjih stopenj. |
Dijak računa s potencami z
racionalnimi eksponenti. |
Dijak preoblikuje koren v potenco z racionalnim
eksponentom in potenco z racionalnim eksponentom v
koren.
Računa s potencami z racionalnimi eksponenti v
številskih in algebrskih izrazih. |
Dijak naj se nauči uporabljati navadno računalo pri
računanju s potencami z racionalnimi eksponenti. |
| 1.2 Kompleksna števila (izbirni tematski sklop) |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Primeri dejavnosti za pouk in priporočila |
Dijak pozna in razume zapis z = a + bi
Ponazori kompleksno število (s točko, z vektorjem) v
kompleksni ravnini. Dijak ponazori množice
kompleksnih števil v kompleksni ravnini. |
Pokažemo potrebo po kompleksnih številih in njihov
pomen v matematiki in stroki. |
| Dijak računa s kompleksnimi
števili. |
Dijak sešteva, odšteva, množi, deli kompleksna števila.
Določi vrednosti potenc imaginarne enote. Določi
konjugirano in absolutno vrednost kompleksnega
števila in oboje ponazori v kompleksni ravnini. |
Povezava – primerjanje : računanje z dvočleniki,
(računanje z vektorji) |
| Dijak uporabi kompleksna
števila (pri reševanju kvadratne
enačbe). |
Dijak reši kvadratno enačbo z realnimi koeficienti in
negativno diskriminanto. Razstavlja izraze v množici
kompleksnih števil. |
|
| 2.1 Osnovni geometrijski pojmi v ravnini in prostoru |
 |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi osnovne
geometrijske pojme o točkah,
premicah in ravninah (iz OŠ). |
|
Učitelj ne poučuje ponovno tistih vsebin, ki sodijo v
pričakovano predznanje dijakov, ampak pripravi
ustrezne dejavnosti za samostojno delo dijakov doma
in/ali v šoli, pri katerih dijaki znanje obnovijo in
dopolnijo. Učitelj diagnosticira napačne predstave in
primanjkljaje ter dijakom pomaga, da jih odpravijo. |
| Dijak sprejme osnovne
aksiome geometrije. |
Dijak pozna aksiome, ki povezujejo točke, premice in
ravnine. |
Pri definicijah geometrijskih pojmov in odnosov med
njimi učitelj uporablja vse načine matematične
govorice:
strokovno neoporečna besedna razlaga, predstavitve s
prostorskimi modeli, z načrtovanjem oz. slikami in s
simbolnim matematičnim zapisom. |
| Dijak ločuje med aksiomi,
izreki, definicijami. |
Dijak ve, da izreki izhajajo iz aksiomov in da z definicijami
opredeljujemo nove pojme, npr. kolinearne točke,
komplanarne točke, konveksne množice točk. |
Dijaki doumejo aksiome kot temeljne matematične
resnice, na katerih sloni geometrija. |
| Dijak uporablja matematični
jezik. |
Dijak uporablja matematični jezik in strokovno
terminologijo pri definiciji pojmov, opisovanju odnosov,
predstavitvi in logični interpretaciji znanih dokazov.
Predstavi in interpretira znan dokaz (npr. izrek(i), ki
govori(jo) o določenosti ravnine).
Ločuje med modeli in koncepti. |
Dijak uporablja matematični jezik pri komuniciranju z
matematiko in o matematiki.
Primerne oblike dejavnosti so samostojni nastopi,
predstavitve, skupinsko delo, projektno delo. |
| Dijak razume pojem kot. |
Dijak pokaže obseg znanja na diagnostičnem preverjanju
v pisni ali ustni obliki. |
Dijaki samostojno ponovijo osnovne pojme o kotu, npr.
izdelajo plakat, napišejo izvlečke, seminarsko nalogo,
pripravijo predstavitev z elektronskimi prosojnicami …
Učitelj diagnosticira in po potrebi dopolni vrzeli v
znanju. |
| Dijak pozna vrste kotov in
odnose med njimi. |
Dijak računa komplementarne in suplementarne kote.
Prepozna in uporablja odnose med koti ob vzporednicah
in koti s pravokotnimi kraki. |
|
| Dijak pozna mere za kot in
računa s koti. |
Dijak nadgradi znanje o kotnih merah, in sicer: računa
tudi s kotno sekundo, spozna radian in zna pretvarjati iz
stopinj v radiane in obratno. Pri tem suvereno uporablja
navadno računalo. Na pamet pretvarja stopinje v radiane
in obratno pri kotih: (npr. 60° ,30° , 45° ,90° ,120°...)
Suvereno računa velikosti kotov. |
Dijaki urijo spretnosti uporabe navadnega računala pri
pretvarjanju kotnih mer: iz desetiškega v šestdesetiški
številski sistem in obratno ter iz kotnih stopinj v radiane
in obratno. |
| Dijak načrtuje kote s šestilom
in geotrikotnikom. |
Dijak načrtuje kote do polnega kota z geotrikotnikom ali s
šestilom glede na stroko oz. poklic. Dijak pozna pojem
simetrale in načrta simetralo daljice in kota tudi pri
uporabi programov dinamične geometrije. |
Izvajajo se le preprostejše klasične geometrijske
konstrukcije (koti, simetrale daljic in kotov) z
geometrijskim orodjem in v obsegu, ki je pomemben za
stroko. |
| Dijak se orientira v
koordinatnem sistemu
(pravokotni in polarni
koordinatni sistem). |
Dijak poveže lego točke v ravnini z oddaljenostjo od
koordinatnih osi (pravokotni koordinatni sistem) in z
oddaljenostjo od izbrane točke (pol) in kotom med
izbrano premico (polaro) in točko. Polarni koordinatni
sistem dijak uporablja le glede na potrebe stroke. Loči
med pozitivno in negativno orientiranimi koti.
Riše in odčitava lego točke v danem koordinatnem
sistemu. |
Vsebine ravninske geometrije se navezujejo na
koordinatni sistem, kjer je to primerno, npr. lega točke,
geometrijske transformacije.
Dijak pri znanih koordinatah nariše točko v danem
koordinatnem sistemu. Polarni koordinatni sistem dijak
uporablja le glede na potrebe stroke.
Programe dinamične geometrije uporabljajo dijaki
predvsem za samostojno raziskovanje. |
| 2.2 Transformacije v ravnini |
Povezani cilji iz OŠ:
Dijak iz 7. razreda pozna lastnosti, načrtuje in simbolno zapiše naslednje preslikave:
Vzporedni premik
Zrcaljenje čez točko ZA: A→ A'
Zrcaljenje čez premico Zp: A→ A' |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi osnovne
preslikave v ravnini iz OŠ. |
Dijak preveri lastnosti neke geometrijske konfiguracije
(npr. raziskuje simetrije). |
Osnovni pojmi iz OŠ se ne poučujejo znova. Dijaki jih s
samostojnim delom ponovijo, učitelj diagnosticira
znanje. |
| Dijak pozna in uporablja še novi
transformaciji v ravnini: vrtež
in središčni razteg. |
Dijak uporablja osnovne transformacije pri raziskovanju
geometrijskih konfiguracij, pri načrtovanju in merjenju.
Izvede osnovne geometrijske transformacije z
geometrijskim orodjem in z opisom oz. zapisom
postopka (npr. zrcaljenje, razteg). |
Izvajajo se le preprostejše klasične geometrijske
konstrukcije z geometrijskim orodjem in v obsegu, ki je
pomemben za stroko. |
| Dijak razume in uporablja
pojma skladnost in podobnost. |
Dijak razume pojma: skladnost daljic in kotov. Pozna
pojem razmerja in pojem sorazmerja daljic.
Uporabi ustrezne strategije in povezuje vsebine
ravninske geometrije (npr. izdelava skice, uvid v
situacijo, analiza odnosov, delitev lika v osnovne dele –
trikotnike, povezovanje likov in koordinatnega sistema). |
Programe dinamične geometrije uporabljajo dijaki
predvsem za samostojno raziskovanje.
Vsebine ravninske geometrije se navezujejo na
koordinatni sistem, kjer je to primerno, npr. lega točke,
geometrijske transformacije. |
| 2.3 Geometrijski liki |
Povezani cilji iz OŠ:
Geometrijski pojmi, ki jih je dijak spoznal do vključno 8. razreda:
- krog in njegovi deli (krožnica, polmer, premer, krožni lok in izsek, središčni kot), medsebojna lega premice in kroga ter dveh krogov (tetiva, sekanta, tangenta, mimobežnica, središčna razdalja), načrtovanje tangente v točki na krožnici;
- trikotnik (vsota notranjih in zunanjih kotov, trikotniška neenakost), vrste trikotnikov glede na stranice in kote, višine trikotnika, težiščnice in težišče, očrtani in včrtani krog, podobni in skladni trikotniki, načrtovanje trikotnika, delitev daljice v predpisanem razmerju;
- štirikotnik (pravokotnik, kvadrat, paralelogram, romb, trapez, enakokraki trapez, deltoid), diagonale, vsota notranjih kotov, načrtovanje paralelograma, romba, enakokrakega trapeza;
- pravilni večkotnik;
- orientacija pri označevanju likov;
- računanje obsegov in ploščin likov;
- merske enote za dolžino, ploščino in prostornino.
|
| Opis ciljev |
Operativni cilji |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi definicije
geometrijskih likov in njihove
lastnosti iz OŠ. |
|
Dijaki samostojno ponovijo osnovne pojme o likih, npr.
izdelajo plakat, napišejo izvlečke, seminarsko nalogo,
pripravijo predstavitev z elektronskimi prosojnicami …
Učitelj diagnosticira in po potrebi dopolni vrzeli v
znanju. |
| Dijak pozna izrek o obodnem in
središčnem kotu. |
Dijak pozna in uporablja zvezo med obodnim in
središčnim kotom nad istim lokom (tudi Talesov izrek v
polkrogu) v načrtovalnih in drugih geometrijskih
problemih.
Načrtuje tangenti na krog skozi točko zunaj kroga. |
Izvajajo se le preprostejše klasične geometrijske
konstrukcije z geometrijskim orodjem in v obsegu, ki je
pomemben za stroko. |
| Dijak pozna odnose med
stranicami in koti trikotnika. |
Dijak uporablja zveze med notranjimi in zunanjimi koti
trikotnika ter računa s koti (npr. zunanji kot je vsota
nepriležnih notranjih kotov trikotnika).
Predstavi in logično interpretira znan dokaz (npr. vsota
notranjih kotov). |
Dijaki samostojno raziskujejo in razvrščajo trikotnike
glede na odnose med stranicami in koti po različnih
kriterijih (npr. na osnovi trikotniške neenakosti,
velikosti kotov, dolžin stranic). |
| Dijak ločuje med skladnima in
podobnima trikotnikoma. |
Dijak pozna aksiom in izreke o skladnih trikotnikih.
Pozna tudi definicijo in izreke za podobne trikotnike. |
Učitelj uvaja in uporablja pojme, odnose in lastnosti pri
reševanju problemov, povezanih s stroko in
življenjskimi situacijami. |
| Dijak načrtuje trikotnike,
štirikotnike in pravilne
večkotnike. |
Dijak načrtuje trikotnike z znanimi podatki o stranicah,
kotih, višinah, težiščnicah in
podobne trikotnike v danem razmerju.
Izvede osnovne konstrukcije z geometrijskim orodjem
in z opisom oz. zapisom postopka. |
Dijak preveri lastnosti neke geometrijske konfiguracije
(npr. razišče, kdaj središče trikotniku očrtanega kroga
leži znotraj trikotnika). |
| Dijak pozna in uporablja
osnovne izreke v ravnini
(Pitagorov, Evklidov, višinski,
Talesov). |
Dijak uporablja osnovne izreke za določanje različnih
elementov v trikotniku, v konstrukcijskih nalogah in pri
reševanju kompleksnejših geometrijskih problemov. |
Obravnava likov in izrekov temelji deloma na deduktivni
metodi in na opisni metodi. |
| 2.4 Kotne funkcije |
Predznanje:
Pravokotni trikotnik, Pitagorov izrek |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak pozna definicije kotnih
funkcij ostrega kota v
pravokotnem trikotniku. |
Dijak računa vrednosti kotnih funkcij (sinus, kosinus,
tangens, kotangens) ostrega kota v pravokotnem
trikotniku in računa kot pri dani kotni funkciji.
Uporablja navadno računalo. Velikosti kotov so merjene
v kotnih stopinjah (minutah, sekundah) ali radianih.
Uporablja točne vrednosti kotnih funkcij za kote
60° ,30° , 45° ,90° ,0° . Dijak uporablja zveze med kotnimi
funkcijami komplementarnih kotov. |
Dijaki računajo vrednosti kotnih funkcij in kote v
obsegu, ki je pomemben za stroko. |
| Dijak predstavlja kotne funkcije
kotov od 0° do 360° z enotsko
krožnico. |
Dijak poveže pravokotni koordinatni sistem z enotsko
krožnico in razume predstavitev vrednosti kotih funkcij
v njej. Uporablja navadno računalo in trigonir. |
Učitelj uporablja različno tehnologijo pri povezovanju
koordinatnega sistema in enotske krožnice. Poudarek je
na razumevanju odnosa med velikostjo kota in
vrednostmi kotnih funkcij ter njihovimi predznaki v
različnih kvadrantih.
Dijaki samostojno preiskujejo in raziskujejo. Pri tem
uporabljajo tudi programe dinamične geometrije v
obsegu, ki je pomemben za stroko. |
| Dijak pozna in uporablja sinusni
in kosinusni izrek. |
Dijak uporablja sinusni in kosinusni izrek za računanje
stranic in kotov trikotnika. Uvidi pomen izrekov, kot
temeljnih orodij za razrešitev kateregakoli trikotnika in
s tem poljubnega večkotnika. Uporablja navadno
računalo. |
Dijaki urijo razreševanje poljubnega trikotnika v
nalogah in problemih iz okolja. |
| Dijak računa polmera trikotniku
včrtanega in očrtanega kroga. |
Dijak uporablja formule za računanje trikotniku
včrtanega in očrtanega kroga. Uporablja navadno
računalo. |
Učitelj poišče primere iz življenja, okolja in stroke. |
| Dijak ponovi merske enote za
dolžino, ploščino, prostornino iz
OŠ. |
Dijak suvereno pretvarja merske enote
za dolžino, ploščino in prostornino. Glede na potrebe
stroke uporablja velike ali male enote, in jih zapiše v
razstavljeni obliki z uporabo faktorja 10n oz. 10-n . Pri
poimenovanju enot dijak uporablja
predpone (npr. nano, mikro, …, mega, giga). |
|
| Dijak računa dolžine daljic,
obsege in ploščine likov. |
Dijak računa obseg in ploščino poljubnega trikotnika in
sestavljenih likov z že znanimi formulami, s Heronovim
obrazcem in formulami, ki vključujejo kotne funkcije.
Uporablja novo oznako za ploščino likov (S). Rešuje
tudi indirektne naloge pri iskanju različnih elementov v
likih (npr. višina, diagonala …).
Računa dolžine stranic tudi z uporabo sorazmerja. Pri
izračunih dijak ocenjuje in kritično presoja dobljene
vrednosti ter je pozoren na merske enote. Uporablja
navadno računalo. |
Poudarek je na razreševanju splošnega trikotnika,
uporabi sinusnega in kosinusnega izreka ter
Heronovega obrazca. |
| Dijak rešuje kompleksne
geometrijske probleme. |
Dijak uporablja ustrezne strategije in povezuje vsebine
ravninske geometrije (npr. izdelava skice, uvid v
situacijo, analiza odnosov, delitev lika v osnovne dele –
trikotnike, povezovanje likov in koordinatnega sistema). |
Dijaki tudi samostojno preiskujejo in raziskujejo. Pri
tem uporabljajo tudi programe dinamične geometrije. |
| 2.5 Geometrijska telesa |
Povezani cilji iz OŠ:
Oglata telesa: kocka, kvader, (pravilna) prizma, (pravilna) 4-strana piramida, osnovni rob, stranski rob, višina (telesa), osnovna ploskev, stranska ploskev, plašč, mreža telesa, površina ( P = 2O + pl, P = O + pl ), prostornina 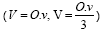
Okrogla telesa: valj ( P = 2πr2 + 2πrv ,V = πr2v ), stožec ( P = πr2 +π rs ,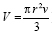 , krogla , krogla
Višina in diagonala stranske ploskve, telesna diagonala, osni presek. |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi osnovne pojme o
geometrijskih telesih iz OŠ. |
|
Dijaki samostojno ponovijo osnovne pojme o telesih,
npr. izdelajo plakat, napišejo izvlečke, seminarsko
nalogo, pripravijo predstavitev z elektronskimi
prosojnicami … Učitelj diagnosticira in po potrebi
dopolni vrzeli v znanju. |
| Prizma in valj |
Dijak razume prizmo kot telo s poljubno osnovno
ploskvijo. Uporablja pojme: diagonala osnovne in
stranske ploskve, telesna diagonala; osni in diagonalni
presek; kot med daljicama in kot med ravninama.
Računa kompleksne naloge z uporabo navadnega
računala. Pri izračunih dijak ocenjuje in kritično presoja
dobljene vrednosti ter je pozoren na merske enote. |
Dijaki izdelujejo modele teles, raziskujejo in rešujejo
naloge s programi dinamične geometrije.
Poiščejo modele teles iz življenja, okolja, stroke in v
zvezi z njimi računajo različne količine. |
| Piramida in stožec |
Dijak razume piramido kot telo s poljubno osnovno
ploskvijo. Uporablja pojme: značilni osni presek; kot
med daljicama in kot med ravninama. Računa
kompleksne naloge z uporabo računala. Pri izračunih
dijak ocenjuje in kritično presoja dobljene vrednosti ter
je pozoren na merske enote. |
Dijaki izdelujejo modele teles, raziskujejo in rešujejo
naloge s programi dinamične geometrije.
Poiščejo modele teles iz življenja, okolja, stroke in v
zvezi z njimi računajo različne količine. |
| Vrtenine in krogla |
Dijak prepozna valj, stožec in kroglo kot vrtenine.
Določi os vrtenja in analizira nastalo vrtenino glede na
izbiro osi. |
Dijaki tudi samostojno preiskujejo in raziskujejo. Pri
tem uporabljajo tudi programe dinamične geometrije |
| Dijak rešuje kompleksne
probleme v prostoru. |
Dijak uporablja ustrezne strategije in povezuje vsebine
prostorske geometrije (npr. izdelava skice, uvid v
situacijo, analiza odnosov, vključevanje pojmov iz
ravninske geometrije in geometrije teles). |
Dijaki tudi samostojno preiskujejo in raziskujejo. Pri
tem uporabljajo tudi programe dinamične geometrije. |
| 2.6 Krivulje II. reda (izbirni tematski sklop) |
Predznanje:
Osnovni geometrijski pojmi: točka, premica, daljica, krožnica (kot geometrijsko mesto točk), simetrala,
Zrcaljenje in simetrije
Koordinatni sistem, linearna in kvadratna funkcija
Enačbe in sistemi enačb |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak spozna krivulje, ki
nastanejo pri preseku stožca in
dvojnega stožca z ravninami. |
Dijak prepozna krivulje, ki nastanejo s presekom
dvojnega stožca z ravninami: krožnica, elipsa,
hiperbola, parabola, z znanjem, ki ga je pridobil pri
strokovnih predmetih, npr. tehničnem risanju,
meritvah. |
Učitelj pomaga povezati matematično predznanje
dijakov z njihovim specifičnim strokovnim predznanjem.
Pri tem uporabi možnosti, ki jih omogoča stroka, npr.
primeri nalog, izdelkov, računalniški programi in druga
tehnologija. |
| Dijak poveže krožnico in
koordinatni sitem. |
Dijak zapiše enačbo krožnice v središčni legi in
premaknjeni legi s središčem S(p,q).
Analizira medsebojne lege krožnice in premice in dveh
krožnic ter računa razdalje in koordinate presečišč. |
Dijaki samostojno preiskujejo in raziskujejo. Pri tem
uporabljajo grafična računala, programe za simbolno
računanje, programe dinamične geometrije in
programe iz stroke. |
| Dijak poveže elipso, hiperbolo,
parabolo in koordinatni sitem. |
Dijak uporablja enačbo elipse in hiperbole v središčni
legi ter parabole s temenom v koordinatnem izhodišču.
Glede na potrebe stroke, uporablja tudi enačbe krivulj,
ki so vzporedno premaknjene za vektor v = ( p, q)
Analizira medsebojne lege krivulj in premic v
koordinatnem sistemu. Pri tem uporablja ustrezne
računalniške programe. |
Dijaki samostojno preiskujejo in raziskujejo. Pri tem
uporabljajo tudi ustrezne računalniške programe, npr.
programe dinamične geometrije in programe iz stroke. |
| 2.7 Vektorji (izbirni tematski sklop) |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak pozna in uporablja
grafično ponazoritev vektorjev. |
Dijak grafično ponazori vektor z usmerjeno daljico.
Nariše vektor z danimi koordinatami a=(a1,a2)
koordinatnem sistemu. Točki v koordinatnem sistemu
določi koordinate krajevnega vektorja. |
Dijak primerja ponazoritev vektorjev v koordinatnem
sistemu s ponazoritvijo kompleksnih števil v kompleksni
ravnini. |
| Dijak sešteva in odšteva
vektorje. Vektor pomnoži s
skalarjem. |
Dijak grafično in računsko sešteva in odšteva vektorje.
Grafično in računsko pomnoži vektor s skalarjem.
Uporablja lastnosti vsote in produkta s skalarjem pri
poenostavljanju izrazov. |
Učitelj pri ponazoritvi vektorjev uporablja različno
tehnologijo (npr. programi dinamične geometrije). |
| Dijak pozna in uporablja pojme
linearna kombinacija vektorjev,
kolinearnost, komplanarnost,
baza. |
Dijak pozna in uporablja pojem linearna kombinacija
vektorjev. Pozna in uporablja pojma kolinearnost in
komplanarnost. Grafično in računsko izrazi dani vektor
kot linearno kombinacijo dveh nekolinearnih vektorjev
(razstavljanje vektorjev). |
Dijak rešuje naloge na elementarnem nivoju.
Učitelj poveže z razstavljanjem sil pri fiziki. |
| Dijak izračuna skalarni produkt
vektorjev. |
Dijak izračuna skalarni produkt vektorjev. Pozna in
uporablja lastnosti skalarnega produkta. Izračuna
dolžino vektorja. Izračuna kot med vektorjema.
Ugotovi, ali sta vektorja vzporedna oziroma
pravokotna. |
Učitelj naj poudari medpredmetne povezave (med
fizikalnimi količinami so na primer vektorji hitrost,
pospešek, sila) in pomen vektorjev v stroki. |
| 3.1 Funkcija in enačba |
Povezani cilji iz OŠ:
Dijak uporablja pravokotni koordinatni sistem v ravnini, upodablja točke v koordinatnem sistemu in jih odčituje.
Dijak opiše odvisnost dveh količin, jo prikaže s tabelo in grafom ter zapiše simbolično. Pozna in uporablja enačbi premega in obratnega sorazmerja.
Dijak zapiše enačbo linearne funkcije, nariše njen graf, iz grafa razbere presečišči s koordinatnima osema in izračuna ničlo linearne funkcije.
Dijak razločuje enačbe od izrazov. V besedilu prepozna linearni odnos in zapiše preprosto linearno enačbo. Reši linearno enačbo, ki lahko vsebuje tudi
oklepaje in številske ulomke. |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi osnovne pojme o
koordinatnem sistemu,
odvisnosti količin,
predstavitvah podatkov,
sorazmerjih, funkcijah in
enačbah (iz OŠ). |
|
Učitelj ne poučuje ponovno tistih vsebin, ki sodijo v
pričakovano predznanje dijakov, ampak pripravi
ustrezne dejavnosti za samostojno delo dijakov doma
in/ali v šoli, pri katerih dijaki predznanje obnovijo in
dopolnijo. Učitelj diagnosticira napačne predstave in
primanjkljaje ter dijakom pomaga, da jih odpravijo. |
| Dijak dopolni znanja o
koordinatnem sistemu. |
Dijak opiše lastnosti pravokotnega koordinatnega
sistema v ravnini. Uporablja ga za prikazovanje lege
množic točk v ravnini. Pozna pojem razdalje med
točkama in njene lastnosti. Določa razdalje med
točkami. |
|
| Dijak pozna definicijo funkcije. |
Dijak pozna splošno definicijo funkcije in definicijo
realne funkcije realne spremenljivke. Uporablja različne
načine predstavitve funkcije: enačbo (funkcijski
predpis), tabelo in graf. |
Različne primere funkcij vpeljemo kot modele
realističnih pojavov iz stroke, drugih predmetnih
področij ali življenja.
Za načrtovanje grafov uporabljamo grafična računala in
računalniške programe. |
| Dijak prepozna lastnosti realnih
funkcij realne spremenljivke. |
Dijak pozna lastnosti surjektivnih, injektivnih in
bijektivnih funkcij. Zapiše definicijsko območje in
zalogo vrednosti funkcije, ugotovi zveznost funkcije,
določi intervale, na katerih je funkcija pozitivna oz.
negativna, določi intervale naraščanja in padanja
funkcije, določi lokalne ekstreme funkcije, ugotovi
sodost oz. lihost funkcije, določi intervale konveksnosti
in konkavnosti funkcije, ugotovi periodičnost funkcije in
določi asimptote. |
Doseganje tega cilja poteka kontinuirano skozi celotno
srednje strokovno izobraževanje.
Pred obravnavo posameznih tipov funkcij dijaki
preučujejo lastnosti funkcij predvsem na osnovi
njihovih grafov in v povezavi z razumevanjem
realističnih pojavov, ki jih funkcijski predpisi
predstavljajo. Pri preučevanju lastnosti funkcij dijaki
uporabljajo grafična računala in računalniške programe.
Na analitični način obravnavamo dane lastnosti pri
poglobljeni obravnavi posameznih tipov funkcij. |
| Dijak izvaja premike in raztege
funkcij. |
Dijak v zapisu funkcije najde osnovno funkcijo in
prepozna premik v smeri abscisne oz. ordinatne osi ter
razteg v smeri abscisne oz. ordinatne osi. S pomočjo
tehnologije nariše graf osnovne funkcije ter grafe
premaknjenih oz. raztegnjenih funkcij. |
Doseganje tega cilja poteka kontinuirano skozi celotno
srednje strokovno izobraževanje.
Pred obravnavo posameznih tipov funkcij dijaki
preučujejo premike in raztege funkcije z grafičnimi
računali in računalniškimi programi ter v povezavi z
razumevanjem realističnih pojavov, ki jih funkcijski
predpisi predstavljajo. |
| Dijak rešuje enačbe, neenačbe
ter sisteme enačb in neenačb s
pomočjo tehnologije. |
Dijak reši enačbo, neenačbo ali sistem enačb oz.
neenačb s pomočjo tehnologije. Razume pojem rešitve
na algebrski in grafični način, preizkusi pravilnost
rešitve, interpretira pot reševanja in pomen rešitve. |
Doseganje tega cilja poteka kontinuirano skozi celotno
srednje strokovno izobraževanje.
Pred obravnavo posameznih tipov enačb, neenačb in
sistemov enačb ali neenačb dijaki pristopajo k
reševanju predvsem na grafični način in v povezavi z
razumevanjem realističnih pojavov, ki jih dani zapisi
predstavljajo. Pri tem uporabljajo grafično računalo in
računalniške programe.
Analitični način reševanja vključimo ob poglobljeni
obravnavi posameznih tipov funkcij, enačb, neenačb ter
sistemov enačb in neenačb. |
| Dijak izdela in uporablja
matematični model. |
Dijak opiše pojav s čim ustreznejšim matematičnim
modelom. Je kritičen pri izbiri in uporabi modela. |
Doseganje tega cilja poteka kontinuirano skozi celotno
srednje strokovno izobraževanje.
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja. Pri iskanju in izdelavi modela
uporabljajo grafično računalo in računalniške programe.
Izdelava in uporaba matematičnih modelov se izvaja pri
večini tematskih sklopov, v temi »Funkcije, enačbe in
diferencialni račun« pa ima še posebno vlogo pri
osmišljanju funkcij, enačb in neenačb. Smiselno jo je
vključiti tudi v medpredmetne projekte, pri katerih
sodeluje učitelj matematike. |
| 3.2 Linearna funkcija in linearna enačba |
Povezani cilji iz OŠ:
Dijak zapiše enačbo linearne funkcije. Pozna pomen koeficientov v zapisu linearne funkcije in to uporablja pri načrtovanju grafa in pri drugih nalogah.
Izračuna ničlo linearne funkcije.
Dijak zapiše enačbo premice v eksplicitni obliki, nariše njen graf ter iz grafa razbere ali izračuna presečišči premice s koordinatnima osema.
V besedilu prepozna linearni odnos in zapiše preprosto linearno enačbo. Reši linearno enačbo, ki lahko vsebuje tudi oklepaje in številske ulomke. |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi znanje o linearni
odvisnosti, linearni funkciji,
grafu linearne funkcije,
eksplicitni enačbi premice in
linearni enačbi. |
|
Učitelj ne poučuje ponovno tistih vsebin, ki sodijo v
pričakovano predznanje dijakov, ampak pripravi
ustrezne dejavnosti za samostojno delo dijakov doma
in/ali v šoli, pri katerih dijaki predznanje obnovijo in
dopolnijo. Učitelj diagnosticira napačne predstave in
primanjkljaje ter dijakom pomaga, da jih odpravijo. |
| Dijak uporablja lastnosti
linearne funkcije. |
Dijak uporablja osnovne lastnosti linearne funkcije in
koeficientov. Na osnovi smernih koeficientov sklepa o
vzporednosti ali pravokotnosti premic in zapiše enačbo
linearne funkcije. |
Dijaki raziščejo za njih nove lastnosti linearne funkcije.
Ob tem uporabljajo grafična računala ali računalniške
programe. |
| Dijak uporablja različne oblike
enačb premic. |
Dijak razločuje funkcijski zapis od enačbe premice.
Pozna eksplicitno, implicitno in segmentno obliko
enačbe premice ter pomen koeficientov v teh enačbah.
Smiselno pretvarja enačbe premic iz ene v drugo
obliko. |
Dijaki rešujejo naloge in probleme, ki osmislijo potrebo
po različnih oblikah enačbe premice. |
| Dijak prepozna in reši linearno
enačbo oz. linearno neenačbo. |
Dijak analitično in s pomočjo tehnologije reši linearno
enačbo oz. neenačbo. Razume pomen rešitve na
algebrski in grafični način, preizkusi pravilnost rešitve
ter interpretira pot reševanja in pomen rešitve. |
Dijaki pri reševanju enačb oz. neenačb ter sistemov
enačb oz. neenačb uporabljajo grafično računalo ali
računalniške programe, in sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje pomena
enačbe oz. neenačbe in rešitve,
- ko dijaki rešujejo enačbe oz. neenačbe, ki izhajajo
iz realističnih problemov in so zato kompleksnejše
ter zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni prvenstvena
aktivnost, ampak je le faza v širši nalogi ali
projektu.
Ko je cilj dejavnosti učenje postopkov za reševanje
enačbe oz. neenačbe, pa je tehnologija lahko
pripomoček za usmerjanje razmišljanja ali preverjanje
rezultata. Če je le mogoče, naj bo reševanje enačb,
neenačb ali sistemov brez tehnologije osmišljeno s
širšim kontekstom. |
| Dijak prepozna in reši sistem
linearnih enačb oz. sistem
linearnih neenačb. |
Dijak analitično in s pomočjo tehnologije reši sistem
linearnih enačb oz. sistem linearnih neenačb. Razume
pomen rešitve na algebrski in grafični način, preizkusi
pravilnost rešitve ter interpretira pot reševanja in
pomen rešitve. |
| Dijak modelira realistične
pojave z linearno funkcijo. |
Dijak opiše pojav z linearno funkcijo. Je kritičen pri
izbiri in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati z linearno funkcijo. Pri iskanju in
izdelavi modela uporabljajo grafično računalo in
računalniške programe. |
| 3.3 Potenčne funkcije in potenčne enačbe |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak prepozna potenčno
odvisnost in jo razlikuje od
drugih vrst odvisnosti. |
Dijak prepozna potenčno odvisnost iz različnih
predstavitev (besedilo, tabela, graf). Razlikuje
potenčno odvisnost od linearne. |
Primere potenčnih funkcij vpeljemo kot modele
realističnih pojavov iz stroke, drugih predmetnih
področij ali življenja. |
| Dijak predstavi potenčno
odvisnost z enačbo. |
Dijak predstavi potenčno odvisnost količin v simbolni
obliki z enačbo f (x) = xn , n∈Z |
Simbolni zapis z enačbo vpeljemo na primerih
realističnih pojavov iz stroke, drugih predmetnih
področij ali življenja. |
| Dijak pozna in uporablja
lastnosti potenčne funkcije. |
Dijak pozna lastnosti potenčnih funkcij ter jih uporablja
pri risanju grafov in drugih nalogah: zveznost potenčne
funkcije, intervale, na katerih je funkcija pozitivna oz.
negativna, intervale naraščanja in padanja funkcije,
lokalne ekstreme funkcije, sodost oz. lihost funkcije ter
intervale konveksnosti in konkavnosti funkcije.
Lastnosti potenčnih funkcij dijak prepozna in preveri na
analitični in grafični način. |
Dijaki v začetku brez tehnologije po točkah narišejo
vsaj en graf osnovne potenčne funkcije. Nato z
grafičnim računalom ali računalniškim programom
narišejo grafe osnovnih potenčnih funkcij in raziščejo
njihove lastnosti. Šele nato lastnosti potenčnih funkcij
obravnavajo tudi na analitični način. |
| Dijak nariše graf potenčne
funkcije. |
Dijak nariše graf potenčne funkcije
f (x) = a(x - p)n + q z upoštevanjem lastnosti
potenčnih funkcij ter premikov in raztegov funkcije.
Razloži končen graf na osnovi upoštevanja premikov in
raztegov osnovnega grafa funkcije. |
Dijaki uporabijo predznanje o premikih in raztegih
funkcije ter z grafičnim računalom ali računalniškim
programom raziščejo grafe premaknjenih in
raztegnjenih potenčnih funkcij. Nato rišejo grafe tudi
brez uporabe tehnologije. |
| Dijak določi inverzno funkcijo
potenčne funkcije in nariše graf
korenske funkcije. |
Dijak analitično in grafično določi inverzno funkcijo
osnovne potenčne funkcije. Pozna lastnosti korenskih
funkcij in nariše graf korenske funkcije. |
Dijaki pri raziskovanju lastnosti korenskih funkcij
uporabljajo tudi grafična računala in računalniške
programe. Za risanje korenskih funkcij, ki vsebujejo
premike in raztege, dijaki uporabljajo tehnologijo. |
| Dijak prepozna in reši potenčno
enačbo oz. potenčno neenačbo. |
Dijak analitično in grafično reši potenčno enačbo oz.
neenačbo. Razume pomen rešitve na algebrski in
grafični način, preizkusi pravilnost rešitve ter
interpretira pot reševanja in pomen rešitve. |
Dijaki analitično reševanje potenčnih enačb oz. neenačb
povezujejo z grafičnim.
Pri reševanju enačb oz. neenačb uporabljajo grafično
računalo ali računalniške programe, in sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje pomena
enačbe oz. neenačbe in rešitve,
- ko rešujejo enačbe oz. neenačbe, ki izhajajo iz
realističnih problemov in so zato kompleksnejše ter
zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni prvenstvena
aktivnost, ampak je le faza v širši nalogi ali
projektu.
Ko je cilj dejavnosti učenje postopkov za reševanje
enačbe oz. neenačbe, pa je tehnologija lahko
pripomoček za usmerjanje razmišljanja ali preverjanje
rezultata. Če je le mogoče, naj bo reševanje enačb oz.
neenačb brez tehnologije osmišljeno s širšim
kontekstom. |
| Dijak modelira realistične
pojave s potenčnimi funkcijami. |
Dijak opiše pojav s potenčno funkcijo. Primerja različne
modele (linearna funkcija, potenčne funkcije) ter je
kritičen pri izbiri in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati s potenčnimi funkcijami. Pri iskanju
in izdelavi modela uporabljajo grafično računalo in
računalniške programe. |
| 3.4 Kvadratna funkcija in kvadratna enačba |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak prepozna kvadratno
funkcijo. |
Dijak razume kvadratno funkcijo kot primer potenčne
funkcije. Razločuje kvadratno odvisnost od drugih vrst
odvisnosti. |
Dijaki ob potenčni funkciji f (x) = a(x - p)2 + q in
njenem grafu spoznajo nove pojme: kvadratna funkcija,
parabola, teme. |
| Dijak pozna in uporablja
lastnosti kvadratne funkcije. |
Pozna in uporablja nove pojme: teme, parabola,
temenska oblika enačbe, splošna oblika enačbe, ničelna
oblika enačbe. Uporablja vse tri oblike enačbe
kvadratne funkcije in smiselno pretvarja eno obliko v
drugo. Pozna pomen konstant v posameznih oblikah
enačbe in na ta način določa teme in ničle kvadratne
funkcije. Pozna in uporablja lastnosti ničel. |
Dijaki raziskujejo možne enačbe kvadratne funkcije.
Izhajajo iz temenske oblike enačbe kvadratne funkcije
f (x) = a(x - p)2 + q in raziščejo še druge oblike enačb
kvadratne funkcije: splošno in ničelno. Raziščejo pomen
koeficientov v posameznih oblikah enačbe.
Raziskovanje poteka vzporedno na grafični in analitični
način. Dijaki uporabljajo grafična računala ali
računalniške programe. |
| Dijak nariše graf kvadratne
funkcije. |
Dijak iz enačbe kvadratne funkcije s preoblikovanjem v
druge ustrezne oblike enačbe določi teme in ničle
funkcije ter nariše graf. |
Dijaki za risanje bolj kompleksnih kvadratnih funkcij
uporabljajo grafična računala in računalniške programe,
dokler se ne naučijo postopkov za izračun ničel. |
| Dijak prepozna in reši
kvadratno enačbo oz. kvadratno
neenačbo. |
Dijak analitično in s pomočjo tehnologije reši kvadratno
enačbo oz. neenačbo. Razume pomen rešitve na
algebrski in grafični način, preizkusi pravilnost rešitve
ter interpretira pot reševanja in pomen rešitve. Razume
in uporablja rešitve kvadratne enačbe kot ničle
kvadratne funkcije. |
Dijaki pri reševanju enačb oz. neenačb uporabljajo
grafično računalo ali računalniške programe, in sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje pomena
enačbe oz. neenačbe in rešitve,
- ko rešujejo enačbe oz. neenačbe, ki izhajajo iz
realističnih problemov in so zato kompleksnejše ter
zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni prvenstvena
aktivnost, ampak je le faza v širši nalogi ali
projektu.
Ko je cilj dejavnosti učenje postopkov za reševanje
enačbe oz. neenačbe, pa je tehnologija lahko
pripomoček za usmerjanje razmišljanja ali preverjanje
rezultata. Če je le mogoče, naj bo reševanje enačb oz.
neenačb brez tehnologije osmišljeno s širšim
kontekstom. |
| Dijak rešuje realistične
probleme in modelira
realistične pojave s kvadratno
funkcijo. |
Dijak rešuje naloge, pri katerih uporablja kvadratno
funkcijo in njene lastnosti, ali kvadratno enačbo oz.
neenačbo. Dijak opiše pojav s kvadratno funkcijo.
Primerja različne modele (linearna funkcija, potenčne
funkcije, kvadratna funkcija) ter je kritičen pri izbiri in
uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati s kvadratno funkcijo. Pri iskanju in
izdelavi modela uporabljajo grafično računalo in
računalniške programe. |
| 3.5 Polinomi |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak prepozna enačbo
polinoma in ustrezno uvršča
polinom v znanja o linearni
funkciji, potenčnih funkcijah in
kvadratni funkciji. |
Dijak razume polinom kot linearno kombinacijo
osnovnih potenčnih funkcij. Ve, da so vrste funkcij, ki
jih je do sedaj obravnaval (linearna funkcija, potenčne
funkcije, kvadratna funkcija), posebni primeri
polinomov. |
Primere polinomov vpeljemo kot razširitev oz.
posplošitev že znanih funkcij (linearne, potenčnih,
kvadratne). Algebrsko predstavitev polinoma
podkrepimo z realističnimi primeri iz stroke, drugih
predmetnih področij ali življenja. |
| Dijak pozna in uporablja
lastnosti polinomov. |
Dijak pozna lastnosti polinomov ter jih uporablja pri
risanju grafov in drugih nalogah: zveznost polinoma,
lastnost ničel polinoma, intervale, na katerih je funkcija
pozitivna oz. negativna, intervale naraščanja in padanja
funkcije, lokalne ekstreme funkcije, intervale
konveksnosti in konkavnosti funkcije ter obnašanje
polinoma pri velikih in malih vrednostih spremenljivke.
Lastnosti polinomov dijak prepozna in preveri na
grafični, nekatere tudi na analitični način. |
Dijaki z grafičnim računalom ali računalniškim
programom narišejo grafe polinomov in raziščejo
njihove lastnosti. Šele nato nekatere obravnavajo tudi
na analitični način (npr. lastnosti ničel). |
| Dijak nariše graf polinoma. |
Dijak določi ničle polinoma in obnašanje polinoma pri
velikih in malih vrednostih spremenljivk ter skicira graf
z upoštevanjem obnašanja grafa v okolici ničel. |
Dijaki določajo ničle polinomov nižjih stopenj in ničle
razcepnih polinomov v glavnem z razcepom ali
Hornerjevim algoritmom, ničle polinomov višjih stopenj
pa s pomočjo grafičnega računala ali računalniških
programov. |
| Dijak modelira realistične
pojave s polinomi. |
Dijak opiše pojav s polinomom. Primerja različne
modele (linearna funkcija, potenčne funkcije, kvadratna
funkcija, polinom višje stopnje) ter je kritičen pri izbiri
in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati s polinomi. Pri iskanju in izdelavi
modela uporabljajo grafično računalo in računalniške
programe. |
| 3.6 Racionalne funkcije |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak prepozna enačbo
racionalne funkcije. |
Dijak razume racionalno funkcijo kot kvocient
polinomov in prepozna njeno enačbo. |
|
| Dijak pozna in uporablja
lastnosti racionalnih funkcij. |
Dijak pozna lastnosti racionalnih funkcij ter jih
uporablja pri risanju grafov in drugih nalogah,
predvsem: lastnost ničel in polov ter asimptoto
racionalne funkcije. Lastnosti racionalne funkcije dijak
prepozna na grafični, nekatere tudi na analitični način
in jih opiše. |
Dijaki z grafičnim računalom ali računalniškim
programom narišejo grafe racionalnih funkcij in
raziščejo njihove lastnosti. Šele nato obravnavajo
lastnosti ničel in polov ter asimptoto tudi na analitični
način. Analitična obravnava služi boljšemu razumevanju
lastnosti racionalne funkcije, ni pa nujno, da dijak
izkazuje znanje na tem nivoju. |
| Dijak nariše graf racionalne
funkcije. |
Dijak nariše graf racionalne funkcije s pomočjo
tehnologije in ga interpretira. |
Dijaki za risanje grafov uporabljajo grafična računala in
računalniške programe. |
| Dijak modelira realistične
pojave s polinomi. |
Dijak opiše pojav z racionalno funkcijo. Primerja
različne modele (linearna funkcija, potenčne funkcije,
kvadratna funkcija, polinom višje stopnje, racionalna
funkcija) ter je kritičen pri izbiri in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati z racionalno funkcijo. Pri iskanju in
izdelavi modela uporabljajo grafično računalo in
računalniške programe. |
| 3.7 Eksponentna funkcija in eksponentna enačba |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak razlikuje eksponentno
odvisnost od drugih vrst
odvisnosti. |
Dijak prepozna in razume eksponentno rast na primerih
iz stroke in življenja — iz besednega opisa ter iz
predstavitve s tabelo ali grafom. Loči eksponentno
funkcijo od potenčne na osnovi zapisa, tabele in grafa
ter pojasni razlike. |
Učitelj v uvodni uri pripravi primere eksponentne rasti iz
področja, ki je dijakom blizu (glasba, biologija ...) |
| Dijak predstavi eksponentno
odvisnost z enačbo. |
Dijak predstavi eksponentno odvisnost količin v
simbolni obliki z enačbo ( f (x) = ax ). |
Odvisnost je lahko podana z besednim opisom, tabelo
ali grafom. |
| Dijak pozna lastnosti
eksponentne funkcije. |
Dijak pozna enačbo eksponentne funkcije
f (x) = ax , a > 0, a ≠ 1 in pomen konstante a. Pozna
definicijsko območje funkcije, zalogo vrednosti,
začetno vrednost in asimptoto. Pozna vpliv osnove a na
naraščanje oz. padanje funkcije. Ve, da je graf
eksponentne funkcije konveksna krivulja. |
Dijaki uporabijo predznanje in raziščejo lastnosti
eksponentne funkcije. Ob tem uporabljajo grafična
računala ali računalniške programe. |
| Dijak nariše graf eksponentne
funkcije. |
Dijak nariše graf eksponentne funkcije
f (x) = kax- p + q, a > 0, a ≠ 1. Razloži končen graf na
osnovi upoštevanja premikov in raztegov osnovnega
grafa funkcije. |
Dijaki narišejo graf eksponentne funkcije
f (x) = ax , a > 0, a ? 1 z upoštevanjem lastnosti
eksponentne funkcije. Graf eksponentne funkcije
f (x) = kax- p + q, a > 0, a ? 1 pa lahko dijaki narišejo z
uporabo tehnologije. |
| Dijak prepozna in reši
eksponentno enačbo oz.
eksponentno neenačbo. |
Dijak analitično in grafično reši eksponentno enačbo oz.
neenačbo. Razume pomen rešitve na algebrski in
grafični način, preizkusi pravilnost rešitve ter
interpretira pot reševanja in pomen rešitve. |
Dijaki analitično reševanje eksponentnih enačb oz.
neenačb povezujejo z grafičnim.
Pri reševanju enačb oz. neenačb uporabljajo grafično
računalo ali računalniške programe, in sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje pomena
enačbe oz. neenačbe in rešitve,
- ko rešujejo enačbe oz. neenačbe, ki izhajajo iz
realističnih problemov in so zato kompleksnejše ter
zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni prvenstvena
aktivnost, ampak je le faza v širši nalogi ali
projektu.
Ko je cilj dejavnosti učenje postopkov za reševanje
enačbe oz. neenačbe, pa je tehnologija lahko
pripomoček za usmerjanje razmišljanja ali preverjanje
rezultata. Če je le mogoče, naj bo reševanje enačb oz.
neenačb brez tehnologije osmišljeno s širšim
kontekstom. Dokler dijaki ne poznajo logaritma,
eksponentne enačbe oz. neenačbe tipa af (x) ≥ b
rešujejo samo z uporabo tehnologije. |
| Dijak modelira realistične
pojave z eksponentno funkcijo. |
Dijak opiše pojav z eksponentno funkcijo. Primerja
različne modele (linearna funkcija, potenčne funkcije,
polinomi, eksponentna funkcija) ter je kritičen pri izbiri
in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke, drugih
predmetov ali življenja, ki se jih da razmeroma
smiselno modelirati z eksponentno funkcijo. Pri iskanju
in izdelavi modela uporabljajo grafično računalo in
računalniške programe. |
| 3.8 Logaritem, logaritemska funkcija in logaritemska enačba |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak razlikuje logaritemsko
odvisnost od drugih vrst
odvisnosti. |
Dijak prepozna in razume logaritemsko rast na primerih
iz stroke in življenja — iz besednega opisa ter iz
predstavitve s tabelo ali grafom. |
Učitelj pripravi primere logaritemske rasti iz
področja, ki je dijakom blizu (logaritemski papir,
potresni sunki, kemija ...) |
| Dijak zapiše logaritemsko
odvisnost z enačbo. |
Dijak predstavi logaritemsko odvisnost količin v
simbolni obliki z enačbo y = logaX. |
Odvisnost je lahko podana z besednim opisom,
tabelo ali grafom. |
| Dijak pozna lastnosti
logaritemske funkcije. |
Dijak pozna enačbo logaritemske funkcije
f (x) = loga x, a > 0, a ≠ 1 , pomen in vpliv konstante a
na naraščanje oz. padanje funkcije. Pozna definicijsko
območje funkcije, zalogo vrednosti, ničlo funkcije in
asimptoto. Ve, da je logaritemska funkcija inverzna k
eksponentni funkciji. |
Dijaki uporabijo predznanje o eksponentni
funkciji in raziščejo lastnosti logaritemske
funkcije. Ob tem uporabljajo grafična računala ali
računalniške programe. |
| Dijak nariše graf logaritemske
funkcije. |
Dijak nariše graf logaritemske funkcije
f (x) =k loga (x - p) + q. Razloži končen graf na osnovi
upoštevanja premikov in raztegov osnovnega grafa
funkcije. |
Dijaki narišejo graf logaritemske funkcije
f (x) = loga x, a >0, a ? 1 z upoštevanjem
lastnosti logaritemske funkcije. Graf logaritemske
funkcije f (x) =k loga (x - p) + q pa lahko dijaki
narišejo z uporabo tehnologije. |
| Dijak pozna definicijo logaritma
in jo uporablja. |
Dijak pozna definicijo in lastnosti logaritma. Uporablja
definicijo logaritma za reševanje eksponentnih enačb
oblike ax = b , ko ni mogoče reševati s sklepanjem.
Uporablja pravila za računanje z logaritmi za
poenostavljanje smiselnih izrazov z logaritmi. |
Dijaki na pamet izračunajo določene logaritme
npr. log2 √2, ln e2 , za ostale uporabljajo
navadno računalo. |
| Dijak izrazi logaritem pri dani
osnovi z logaritmom pri
poljubni osnovi. |
Dijak pozna in uporablja formulo za prehod k novi
osnovi. |
|
| Dijak prepozna in reši
logaritemsko enačbo oz.
logaritemsko neenačbo. |
Dijak analitično in grafično reši preprosto logaritemsko
enačbo oz. neenačbo. Razume pomen rešitve na
algebrski in grafični način, preizkusi pravilnost rešitve
ter interpretira pot reševanja in pomen rešitve. |
Dijaki analitično reševanje logaritemskih enačb oz.
neenačb povezujejo z grafičnim.
Pri reševanju enačb oz. neenačb uporabljajo
grafično računalo ali računalniške programe, in
sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje
pomena enačbe oz. neenačbe in rešitve,
- ko rešujejo enačbe oz. neenačbe, ki izhajajo iz
realističnih problemov in so zato
kompleksnejše ter zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni
prvenstvena aktivnost, ampak je le faza v širši
nalogi ali projektu.
Ko je cilj dejavnosti učenje postopkov za
reševanje enačbe oz. neenačbe, pa je tehnologija
lahko pripomoček za usmerjanje razmišljanja ali
preverjanje rezultata. Če je le mogoče, naj bo
reševanje enačb oz. neenačb brez tehnologije
osmišljeno s širšim kontekstom. |
| Dijak modelira realistične
pojave z logaritemsko funkcijo. |
Dijak opiše pojav z logaritemsko funkcijo. Primerja
različne modele (linearna funkcija, potenčne funkcije,
eksponentna funkcija, logaritemska funkcija) ter je
kritičen pri izbiri in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke,
drugih predmetov ali življenja, ki se jih da
razmeroma smiselno modelirati z logaritemsko
funkcijo. Pri iskanju in izdelavi modela uporabljajo
grafično računalo in računalniške programe. |
| 3.9 Kotne funkcije |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak pozna in uporablja
definicije kotnih
poljubni kot. |
Dijak pozna in uporablja definicije kotnih funkcij na
enotski krožnici za določitev vrednosti posamezne
kotne funkcije poljubnega kota, podanega v stopinjah
ali radianih. |
Dijaki s pomočjo na enotsko krožnico vrišejo
vrednost posamezne kotne funkcije za poljubni
kot in obratno. Če je dana vrednost ene funkcije,
poiščejo kot in vrednosti drugih funkcij.
Uporabljajo navadno računalo in trigonir. |
| Dijak pozna in uporablja
osnovne zveze med kotnimi
funkcijami istega kota. |
Dijak uporabi osnovne zveze med kotnimi funkcijami in
z dano kotno funkcijo izrazi preostale kotne funkcije. |
Dijaki poenostavljajo izraze in dokazujejo
preproste enakosti z uporabo pravil za
periodičnost, sodost oz. lihost in z uporabo
adicijskih izrekov v obsegu, ki je pomemben za
stroko. |
| Dijak pozna in uporablja
periodičnost ter sodost oz.
lihost kotnih funkcij. |
Dijak s pomočjo periodičnosti ter sodosti oz. lihosti
izrazi kotno funkcijo poljubnega kota s kotno funkcijo
ostrega kota. |
| Dijak pozna in uporablja
adicijske izreke. |
Dijak pozna in uporablja adicijske izreke pri prehodu na
ostri kot, pri dvojnih kotih in dokazovanju drugih
enakosti. |
| Dijak pozna lastnosti kotnih
funkcij. |
Dijak pozna enačbe kotnih funkcij
f (x) = sin x, f (x) = cos x, f (x) = tgx, f (x) = ctgx ter
njihovo definicijsko območje in zalogo vrednosti.
Zapiše ničle, intervale naraščanja in padanja kotnih
funkcij, maksimume in minimume za funkciji sinus in
kosinus ter asimptote za funkciji tangens in kotangens. |
Dijaki v začetku brez tehnologije po točkah
narišejo grafe osnovnih kotnih funkcij. Nato
uporabijo predznanje in z grafičnim računalom ali
računalniškim programom narišejo poljubne grafe
kotnih funkcij ter raziščejo njihove lastnosti. Šele
nato lastnosti kotnih funkcij obravnavajo tudi na
analitični način. |
| Dijak nariše graf kotne funkcije. |
Dijak nariše grafe kotnih funkcij
f (x) = A sin(ω(x - φ))+ y0 ,
f (x) = A cos(ω(x - φ))+ y0 , f (x) = tgx in f (x) = ctgx
Razloži končen graf na osnovi upoštevanja premikov in
raztegov osnovnega grafa funkcije. |
Dijaki narišejo grafe kotnih funkcij
f (x) = sin x, f (x) = cos x, f (x) = tgx, f (x) = ctgx
z upoštevanjem lastnosti funkcij. Grafe funkcij
f (x) = A sin(ω(x - φ))+ y0 in
f (x) = A cos(ω(x - φ))+ y0 pa lahko dijaki
narišejo z uporabo tehnologije. |
| Dijak modelira realistične
pojave s kotnimi funkcijami. |
Dijak opiše pojav s kotno funkcijo. Primerja različne
modele (linearna funkcija, potenčne funkcije,
eksponentna funkcija, polinomi, racionalna funkcija,
logaritemska funkcija, kotna funkcija) ter je kritičen pri
izbiri in uporabi modela. |
Dijaki obravnavajo realistične pojave iz stroke,
drugih predmetov ali življenja, ki se jih da
razmeroma smiselno modelirati s kotnimi
funkcijami. Pri iskanju in izdelavi modela
uporabljajo grafično računalo in računalniške
programe. |
| 3.10 Krožne funkcije in trigonometrijske enačbe (izbirni tematski sklop) |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak pozna in uporablja krožne
funkcije. |
Dijak pozna definicijsko območje in zalogo vrednosti
krožnih funkcij: f (x) = arcsin x, f (x) = arccos x,
f (x) = arctgx, f (x) = arcctgx
Uporablja krožne funkcije za izračun kota v stopinjah in
radianih. |
Dijaki skicirajo graf posamezne krožne funkcije in
zapišejo njene lastnosti. Pri iskanju kota dijaki
uporabljajo računala. |
| Dijak nariše krožno funkcijo. |
Dijak nariše krožno funkcijo kot inverzno funkcijo h
kotni funkciji. Pojasni sliko krožne funkcije na osnovi
razumevanja grafov inverznih funkcij. |
Dijaki narišejo kak primer krožne funkcije brez
tehnologije s ciljem, da bolje razumejo pojem
inverzne funkcije. Za nadaljnje risanje krožnih
funkcij pa uporabljajo grafična računala ali
računalniške programe. |
| Dijak prepozna in reši
trigonometrijsko enačbo oz.
neenačbo. |
Dijak analitično in grafično reši preprosto
trigonometrijsko enačbo oz. neenačbo. Razume pomen
rešitve na algebrski in grafični način, preizkusi
pravilnost rešitve ter interpretira pot reševanja in
pomen rešitve. |
Dijaki rešijo trigonometrijsko enačbo npr.
sin(ωx + ρ), -1 ≤ a ≤ 1, tan 2x = a, sin x = cos x, cos2 x = 1 + sin x, ...
Pri reševanju enačb oz. neenačb uporabljajo
grafično računalo ali računalniške programe, in
sicer:
- ko se učijo reševanja enačb oz. neenačb s
tehnologijo,
- ko je cilj dejavnosti boljše razumevanje
pomena enačbe oz. neenačbe in rešitve,
- ko rešujejo enačbe oz. neenačbe, ki izhajajo iz
realističnih problemov in so zato
kompleksnejše ter zahtevnejše,
- ko reševanje enačbe oz. neenačbe ni
prvenstvena aktivnost, ampak je le faza v širši
nalogi ali projektu.
Ko je cilj dejavnosti učenje postopkov za
reševanje enačbe oz. neenačbe, pa je tehnologija
lahko pripomoček za usmerjanje razmišljanja ali
preverjanje rezultata. Če je le mogoče, naj bo
reševanje enačb oz. neenačb brez tehnologije
osmišljeno s širšim kontekstom. |
| 3.11 Diferencialni račun |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak ponovi znanje o zveznosti
funkcij. |
Dijak nariše graf funkcije. Določi točke nezveznosti.
Prepozna zveznost oz. nezveznost v danih točkah. |
Zveznost se definira opisno. Dijaki ponovijo znanje o
funkcijah, ki so jih spoznali v času izobraževanja ter
določijo zveznost oz. nezveznost v danih točkah.
Dijaki rišejo grafe funkcij na osnovi poznavanja
lastnosti funkcij, pa tudi grafičnimi računali in
računalniškimi programi. |
| Dijak pozna definicijo limite
funkcije. |
Dijak spozna pojma: okolica točke, limita funkcije v
točki. Opiše limito funkcije. Spozna definicije limite in
jih uporablja v danih nalogah. |
Dijaki ponovijo pojem odprtega intervala (odseka na
številski premici) in ga povežejo s pojmom okolica
točke. S pomočjo grafa funkcije določijo limito. Pri tem
lahko uporabljajo grafična računala ali računalniške
programe. |
| Dijak določa limite funkcij. |
Dijak izračuna preproste limite funkcij. Uporablja
pravila za računanje z limitami. |
Dijaki ponovijo razcepe izrazov in jih uporabljajo pri
določanju limit. |
| Dijak določa naklon premice in
kot med premicama. |
Dijak pozna in uporablja zvezo med naklonom premice
in njenim smernim koeficientom.
Določi velikost naklonskega kota premice in velikost
kota med premicama. |
Dijaki raziščejo zvezo med naklonom premice in njenim
smernim koeficientom z grafičnim računalom ali
računalniškimi programi. |
| Dijak pozna definicijo odvoda
funkcije v točki ter razume in
uporablja geometrijski pomen
odvoda. |
Dijak zapiše diferenčni količnik in definicijo odvoda
funkcije. Razume in uporablja zvezo med odvodom
funkcije, naklonom funkcije (oz. tangente na njen graf)
ter rastjo funkcije v okolici dane točke. Določi približno
numerično vrednost odvoda funkcije v točki.
Dijak določi enačbo tangente na graf krivulje v dani
točki in kot med krivuljama. |
Dijaki s pomočjo grafičnega računala ali računalniških
programov raziskujejo povezavo med odvodom,
naklonom tangente in rastjo funkcije v dani točki.
Enačbe tangent in kote med krivuljama določajo
predvsem z namenom boljšega razumevanja povezav
med odvodom, naklonom tangente in rastjo funkcije v
dani točki. |
| Dijak določa odvode funkcij. |
Dijak spozna pojem odvod funkcije. Uporablja pravila
za odvajanje osnovnih in sestavljenih funkcij. Spozna
in uporablja odvode elementarnih funkcij. |
Dijaki ob učiteljevi pomoči razvijejo nekatera pravila za
odvajanje in odvode nekaterih elementarnih funkcij.
Ostala pravila za odvajanje in odvode elementarnih
funkcij sprejmejo od učitelja ali iz literature.
Pri določanju odvodov funkcij je poudarek na
razumevanju odvodov funkcij. Dijaki razvijajo spretnost
določanja odvodov le toliko, da lahko nadaljujejo z
nadaljnjo analizo funkcij. Za določanje odvodov
uporabljajo tudi grafična računala ali računalniške
programe. |
| Dijak uporablja zvezo med
odvodom in lokalnim vedenjem
funkcije. |
Dijak pozna povezavo prvega odvoda funkcije s
stacionarnimi točkami funkcije in z naraščanjem oz.
padanjem funkcije. Uporablja te povezave za določanje
stacionarnih točk, intervalov naraščanja oz. padanja
funkcije ter za reševanje preprostih ekstremalnih
problemov. |
Dijaki rešujejo realistične ekstremalne probleme iz
stroke, drugih področij ali življenja. Pri tem uporabljajo
grafična računala in računalniške programe.
Ob reševanju realističnih primerov dobijo uvid v pomen
odvoda v različnih strokah in učitelj ga zato lahko
utemeljeno poudari. |
| Dijak nariše graf funkcije. |
Dijak razišče lastnosti funkcije. Določi definicijsko
območje funkcije, zalogo vrednosti, intervale
naraščanja in padanja funkcije, lokalne ekstreme in
vodoravne prevoje funkcije. Nariše graf funkcije in ga
interpretira. |
Dijaki za raziskovanje lastnosti funkcije in risanje grafa
uporabljajo tudi grafična računala in računalniške
programe. |
| 3.12 Zaporedja |
| Operativni cilji |
Opis ciljev |
Primeri dejavnosti za pouk in priporočila |
| Dijak pozna definicijo in
lastnosti zaporedja. |
Dijak razume zaporedje kot funkcijo, ki preslika (pod)
množico naravnih števil v neko drugo množico. Določi
lastnosti zaporedja in pozna različne predstavitvene
oblike zaporedij (splošni člen, rekurzijski obrazec,
naštevanje členov, graf). Loči med grafi realnih funkcij
(krivulje) ter grafom zaporedja (točkovni graf). |
Učitelji poiščejo primere iz različnih področij stroke,
življenja in okolja ter pripravijo dejavnosti, pri katerih
dijaki spoznajo zaporedja kot pomembno orodje za
analizo različnih pojavov.
Dijaki dojamejo zaporedja tudi kot specifičen primer
vzorcev v matematiki.
Pri samostojnem raziskovanju in analizah uporabljajo
različno tehnologijo. |
| Dijak pozna in uporablja
definicijo aritmetičnega
zaporedja. |
Dijak definira aritmetično zaporedje, zapiše splošni
člen, določi člene danega zaporedja. Izračuna vsoto n
členov aritmetičnega zaporedja. |
Definicijo zaporedja in izračun vsote n členov
zaporedja lahko vpeljemo s primeri iz zgodovine, stroke
in podobno. |
| Dijak pozna in uporablja
definicijo geometrijskega
zaporedja. |
Dijak razume definicijo geometrijskega zaporedja in
njegove lastnosti ter računa različne količine (splošni
člen, količnik, vsoto). Dojame pomen in uporabnost
geometrijskega zaporedja pri modeliranju različnih
pojavov (npr. v naravi: eksponentna rast, v finančni
matematiki: obrestno-obrestni račun). |
Pri analiziranju in samostojnem raziskovanju pojavov
dijaki uporabljajo tehnologijo in različne računalniške
programe, tudi iz stroke. |
Minimalne standarde znanja izkazuje dijak, ki razvije kompetence le do osnovnih stopenj ter je pri njihovem izkazovanju nesamostojen in manj zanesljiv.
Didaktična priporočila so zapisana kot usmeritve za pouk matematike v III. poglavju (Usmerjevalni cilji, ključne kompetence, usmeritve za razvijanje ključnih kompetenc) in kot bolj konkretna priporočila v zadnji koloni tabel v IV. poglavju (Operativni cilji).
